Reducing Dynamic Power in Booth-Encoded Multipliers Through Zero Representation Selection

Introduction

Radix-4 Modified Booth encoding is widely used in high-performance multipliers to reduce the number of partial products by half. The standard implementation, documented in numerous academic papers, one of which in the References section, uses one’s complement for negative multiples along with S (sign) and E (extension) correction bits for each partial product. This article presents a power optimization technique that exploits the dual representation of zero in one’s complement arithmetic: by selecting +0 (all zeros) instead of −0 (all ones) for the 111 multiplier case, we significantly reduce switching activity in the partial product reduction network without eliminating the need for S and E bits.

The Standard Approach: One’s Complement with Correction

Modified Booth encoding examines three consecutive multiplier bits to generate partial products:

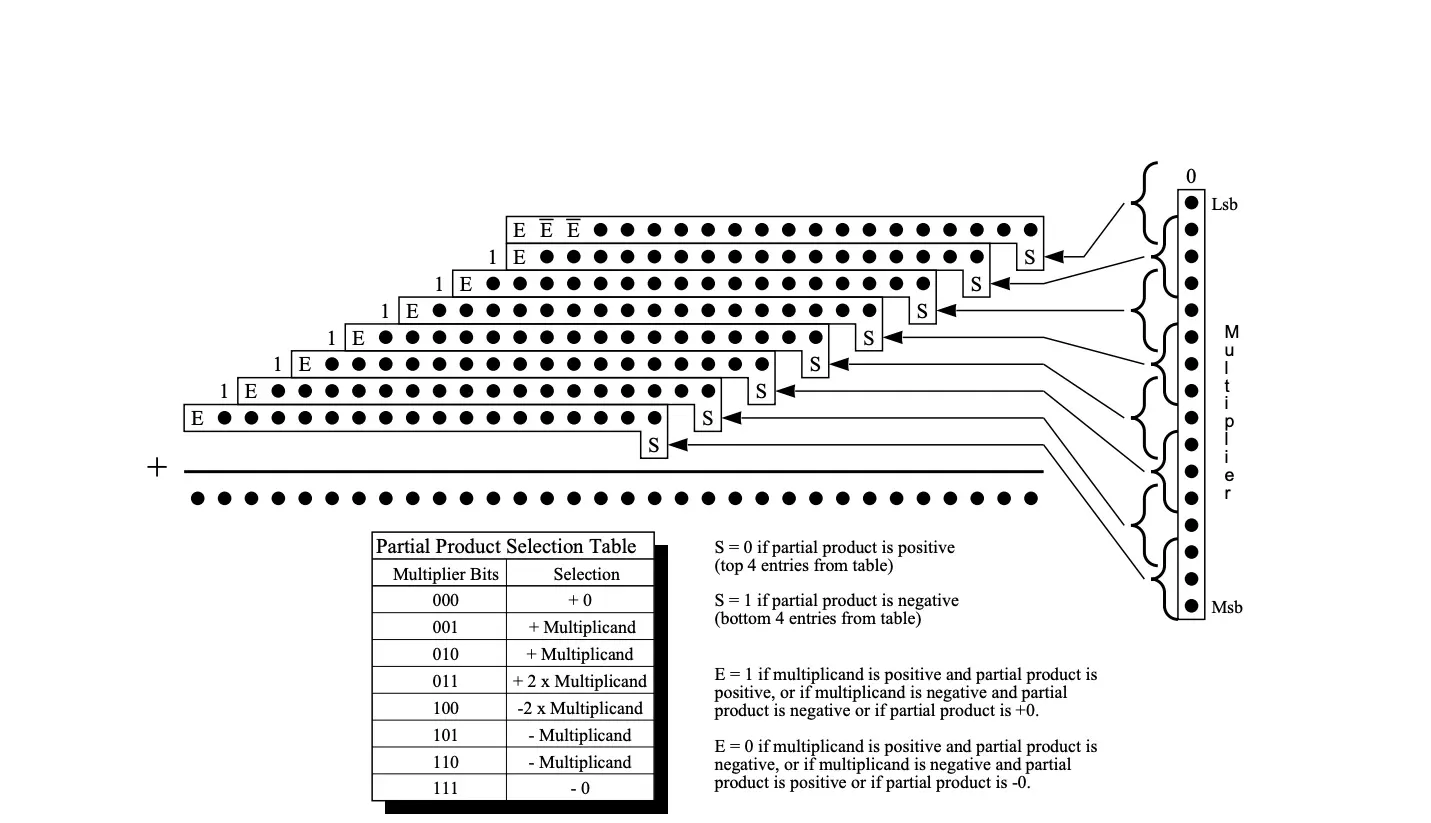
The Traditional Approach with Correction Bits

Computing negative multiples in two’s complement requires: −M = ~M + 1

This is expensive (carry propagation, power consumption), so the standard technique uses one’s complement instead: −M ≈ ~M

The one-bit difference requires correction, which is handled through S and E bits as shown in the diagram:

S (Sign bit):

S = 0 if partial product is positive (top 4 table entries)
S = 1 if partial product is negative (bottom 4 table entries)
Injected into the carry-save adder tree to handle sign extension

E (Extension bit):

Provides proper sign extension based on multiplicand sign and partial product type
Ensures correct two’s complement behavior in the final sum
Also injected into subsequent partial product positions

For the 111 case (which should produce −0), the traditional approach generates:

An all-ones partial product (~M for M=0, which is all 1s)
S and E correction bits to make the final result mathematically zero

The power problem: This all-ones pattern propagates through the entire partial product reduction network (Wallace/Dadda tree), causing significant switching activity even though the mathematical result is zero.

Power Optimization: Selecting +0 Over −0

Here’s the key insight for power reduction:

In one’s complement, zero has two representations: +0 (all zeros) and −0 (all ones). Mathematically, +0 = −0 = 0, even though their bit patterns differ.

This means for the 111 multiplier case:

Traditional: Generate −0 as all-ones pattern, let S/E bits correct it to zero
Optimized: Generate +0 as all-zeros pattern directly

Both approaches are mathematically correct and still require S and E bits for the carry-save tree, but the optimized approach dramatically reduces switching activity.

Why This Reduces Power

When the multiplier window is 111:

Traditional approach:
- Partial product = all 1s (width+1 bits toggling from 0→1)
- These propagate through carry-save adder tree
- Multiple full-adder stages toggle
- S and E bits eventually correct the result to zero
- High switching activity for a mathematically zero contribution
Optimized approach:
- Partial product = all 0s (minimal toggling)
- Zeros propagate through carry-save adder tree (reduced toggling)
- Full-adders and Carry-Save adders see fewer input transitions
- S and E bits still present for proper tree operation
- Minimal switching activity for the same zero contribution

The S and E bits are still computed and injected—they’re necessary for the carry-save adder tree to function correctly. The optimization is recognizing that we can choose which zero representation to send into the tree, and selecting all-zeros instead of all-ones saves substantial power.

Here’s a SystemVerilog Implementation for the above Booth Encoding Algorithm.